M6S6_RE (STE)
Conditions d’achèvement
Consulter
Tu dois parcourir l'ensemble des chapitres de ce cahier de ressources pour bien te préparer au test de validation de cette station.
3. L'énergie mécanique
3.1 Définition de l'énergie mécanique
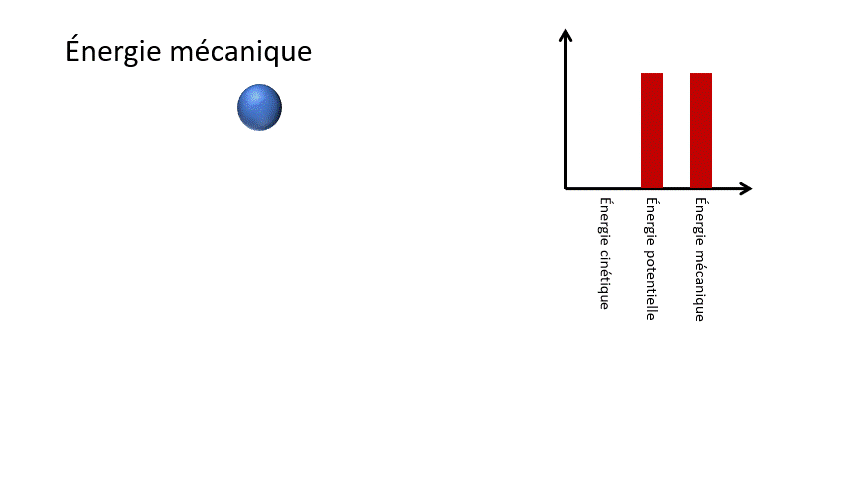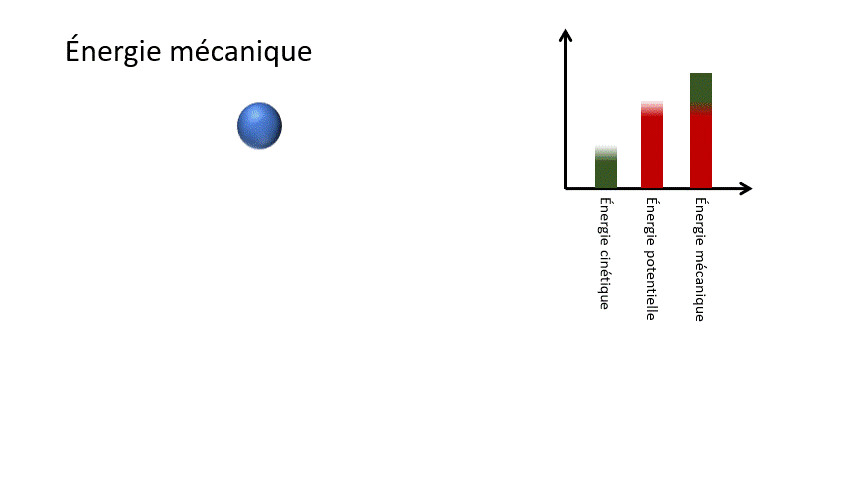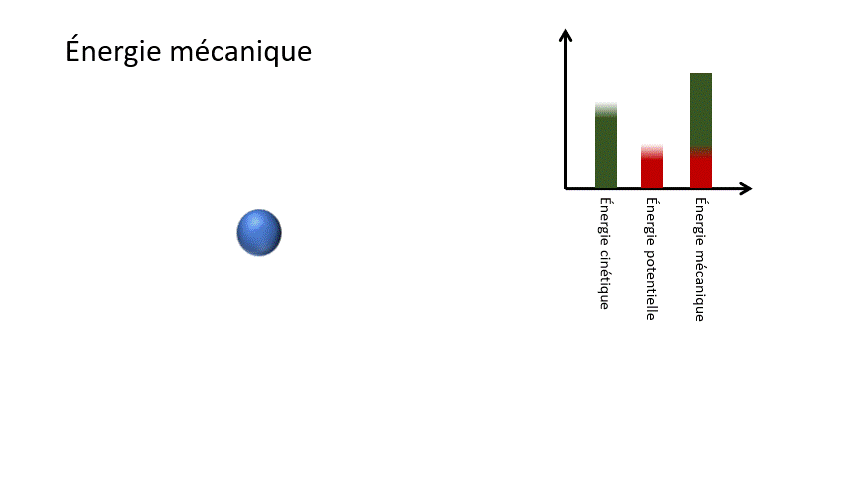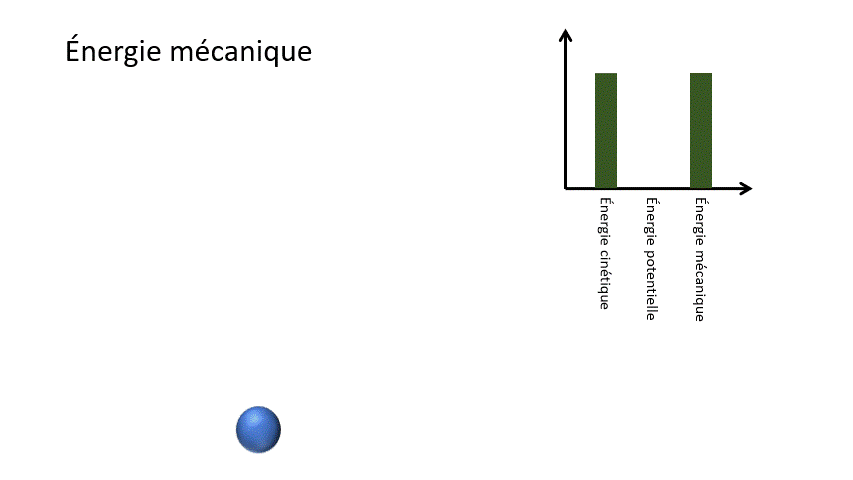
Pour un corps en chute libre, l'énergie potentielle gravitationnelle liée à la hauteur de l'objet est transformée en énergie cinétique liée à la vitesse de celui-ci. Ainsi, l'objet accélère dans sa chute.
Formule
Em = Ek + Ep
Em : Énergie mécanique (J)
Ek : Énergie cinétique (J)
Ep : Énergie potentielle (J)
2.2 Exemples
Exemple 1
Un homme tient une boîte du haut de la fenêtre de son appartement situé au 5ième étage. La boîte en question pèse 15 kg et la hauteur de la fenêtre est à environ 30 mètres du sol. S'il laisse tomber la boîte, quelle sera l'énergie cinétique de la boite à 10 m du sol ?
m = 15 kg
g = 9,8N/kg
h1 = 30 m
h2 = 10 m
Ek1 = 0J
Ek2 = ?
1. Calcul de l'énergie potentielle à 30 m
Ep1 = mgh1
Ep1 = 15 kg x 9,8 N/kg x 30 m = 4 410 J
2. Calcul de l'énergie potentielle à 10 m
Ep2 = mgh2
Ep2 = 15 kg x 9,8 N/kg x 10 m = 1470 J
3. Calcul de l'énergie cinétique à 10 m
Comme il y a conservation de l'énergie, on peut dire que :
Em1 = Em2
Ek1 + Ep1 = Ek2 + Ep2
0 J + 4 410 J = Ek2 + 1470 J
Ek2 = 4 410 J - 1 470 J = 2 940 J
Exemple 2
Quelle sera la vitesse de la boîte lorsqu'elle atteindra le sol ?
m = 15 kg
g = 9,8N/kg
h1 = 30 m
Ep2 = 0J
Ek1 = 0J
v2 = ?
1. Calcul de l'énergie cinétique au sol
Comme il y a conservation de l'énergie, on peut dire que :
Em1 = Em2
Ek1 + Ep1 = Ek2 + Ep2
0 J + 4 410 J = Ek2 + 0 J
Ek2 = 4 410 J
2. Calcul de la vitesse
Ek2 = ½ mv2²
4 410 J = ½ x 15 kg x v2²
392 = v22
v2 = \(\huge{ \sqrt[]{392} m/s }\)
v = 19,8 m/s