Imprimer tout le livreImprimer tout le livre

M6S6_RE (STE)

Site: Moodle CSSRDN
Cours: Science 4e secondaire (ST / STE) - 2023-2024 - Douance
Livre: M6S6_RE (STE)
Imprimé par: Visiteur anonyme
Date: vendredi 18 juillet 2025, 01:58

Description

Tu dois parcourir l'ensemble des chapitres de ce cahier de  ressources pour bien te préparer au test de validation de cette station.

Table des matières

1. L’énergie cinétique

1.1 Définition de l'énergie cinétique

L’énergie cinétique est l’énergie que possède un objet pendant qu’il bouge.

Pour qu’un objet commence à bouger, on doit d’abord faire un travail sur lui pour qu’une force suffisante lui permette de se mettre en mouvement.


La quantité d’énergie cinétique d’un objet va dépendre de deux facteurs :

  • La masse de cet objet (en kg)
  • La vitesse à laquelle l’objet se déplace (en m/s)
    • Description

On calcule l’énergie cinétique à partir de la formule suivante :

Formule

Ek = ½ mv²

m : Masse de l'objet (kg)
v : Vitesse de l'objet (m/s)
Ek : Énergie cinétique (J)

1.2 Exemples

Exemple 1

Une voiture de 2000 kg roule à une vitesse de 40 km/h. Quelle est son énergie cinétique?

m = 2000 kg
v = 40 km/h
Ek = ?

1. Transformer la vitesse ne m/s. 
\(\huge{  \frac{40 km}{1 h} = \frac{40 000 m}{3600 s} = 11,1 m/s} \)


2. Trouver l'énergie cinétique

Ek = ½ mv²

Ek = ½ x 2000 kg x (11,1 m/s)² = 123 210 J
Exemple 2
Et quelle énergie cinétique sera-t-il nécessaire pour faire passer la même voiture à 80 km/h?

m = 2000 kg
v = 80 km/h
Ek1 = 123 310 J
Ek2 = ?
ΔEk = ?

1. Transformer la vitesse ne m/s. 
\( \huge{\frac{80 km}{1 h} = \frac{80 000 m}{3600 s} = 22,2 m/s} \)


2. Trouver l'énergie cinétique

Ek = ½ mv²
Ek = ½ x 2000 kg x  22,2 m/s)² = 492 840 J


3. Trouver la variation d'énergie

∆Ek = Ek2 - Ek1 = 492 840 J - 123 210 J = 369 630 J

Les utilisateurs invités n’ont pas la permission d’interagir avec des questions intégrées.

Les utilisateurs invités n’ont pas la permission d’interagir avec des questions intégrées.



Clique sur le bouton ci-dessous afin de poursuivre au chapitre suivant.

Continuer  

2. L'énergie potentielle

2.1 Définition de l'énergie potentielle

On définit l’énergie potentielle comme l’énergie emmagasinée par un objet en fonction de sa position ou sa forme. Dans le cas précis qui nous intéresse ici, il s’agit de l’énergie potentielle gravitationnelle qui se concentre sur la hauteur de l’objet par rapport au sol. Celle-ci est proportionnelle à trois facteurs :

  • La masse de l’objet (en kg)
  • L’intensité du champ gravitationnel (9,8 N/kg sur la Terre)
  • La hauteur de l’objet (en m).
    • Description

On calcule l’énergie potentielle grâce à cette formule :

Formule

Ep = mgh

m : Masse de l'objet (kg)
g : Intensité du champ gravitationnel (N/kg)
h : Hauteur (m)
Ep : Énergie potentielle (J)

2.2 Exemples

Exemple 1

Un homme tient une boîte du haut de la fenêtre de son appartement situé au 5ième étage. La boîte en question pèse 15 kg et la hauteur de la fenêtre est à environ 30 mètres du sol. Quelle est l’énergie potentielle gravitationnelle contenue dans la boîte?

m = 15 kg
h = 30m
g = 9,8 N/kg
Ep = ? J
Ep = mgh

Ep = 15 kg x 9,8 N/kg x 30 m = 4 410 J
Exemple 2
L’homme laisse tomber la boîte. Quelle est  l’énergie potentielle à 20 m et 10 m du sol.

m = 15 kg
g = 9,8 N/kg
h1 = 10 m
Ep1 = ? J
h2 = 20 m
Ep2 = ? J

1. Énergie potentielle à 20 m

Ep = mgh

Ep = 15 kg x 9,8 N/kg x 20 m = 2 940 J



2. Énergie potentielle à 10 m
Ep = mgh

Ep = 15 kg x 9,8 N/kg x 10 m = 1 470 J

Comme on peut le constater, l’énergie potentielle diminue au fur et à mesure que la boîte s’approche du sol.

Les utilisateurs invités n’ont pas la permission d’interagir avec des questions intégrées.

Les utilisateurs invités n’ont pas la permission d’interagir avec des questions intégrées.

Les utilisateurs invités n’ont pas la permission d’interagir avec des questions intégrées.


Peut-on prédire la vitesse de la boîte si on en connait la hauteur ? C'est ce que nous verrons dans la prochaine section portant sur l'énergie mécanique. 

Clique sur le bouton ci-dessous afin de poursuivre au chapitre suivant.

Continuer   

3. L'énergie mécanique

3.1 Définition de l'énergie mécanique

La mécanique est la partie de la physique qui se penche sur l’étude des mouvements et des états d’équilibre des objets. L’énergie mécanique est donc le total des énergies cinétique et potentielle. L'application suivante illustre bien le lien entre les énergies mécanique, cinétique et potentielle. 


Les utilisateurs invités n’ont pas la permission d’interagir avec des questions intégrées.


Pour un corps en chute libre, l'énergie potentielle gravitationnelle liée à la hauteur de l'objet est transformée en énergie cinétique liée à la vitesse de celui-ci. Ainsi, l'objet accélère dans sa chute. 
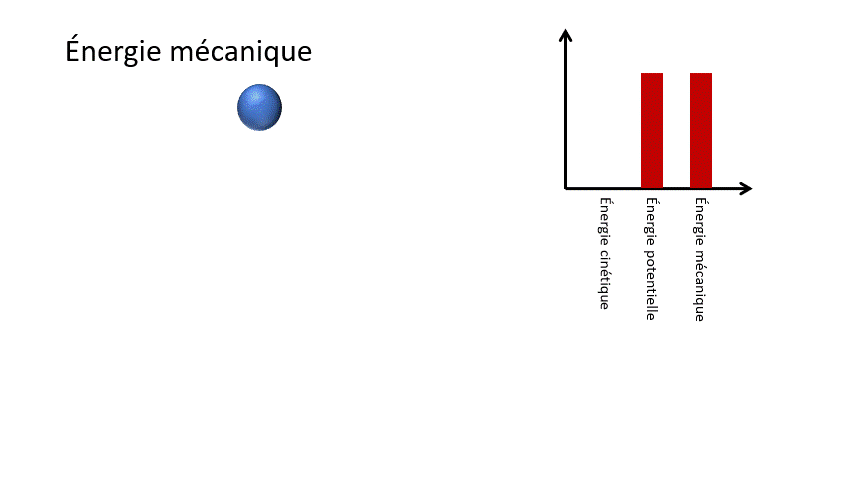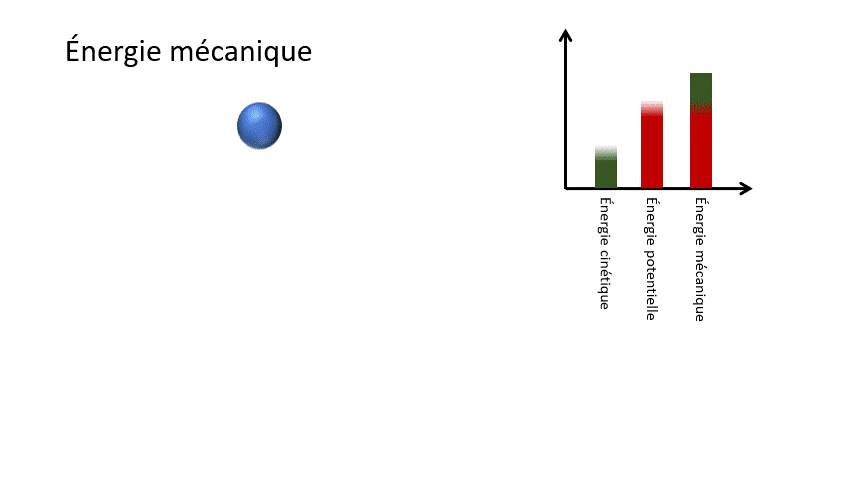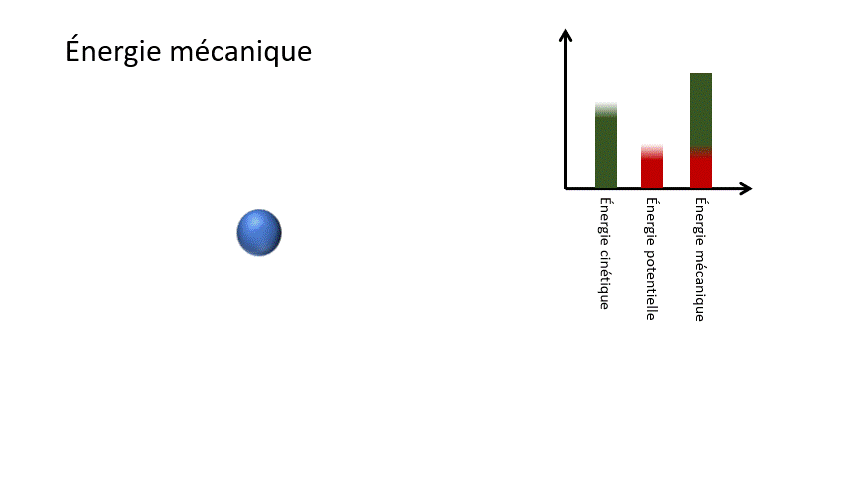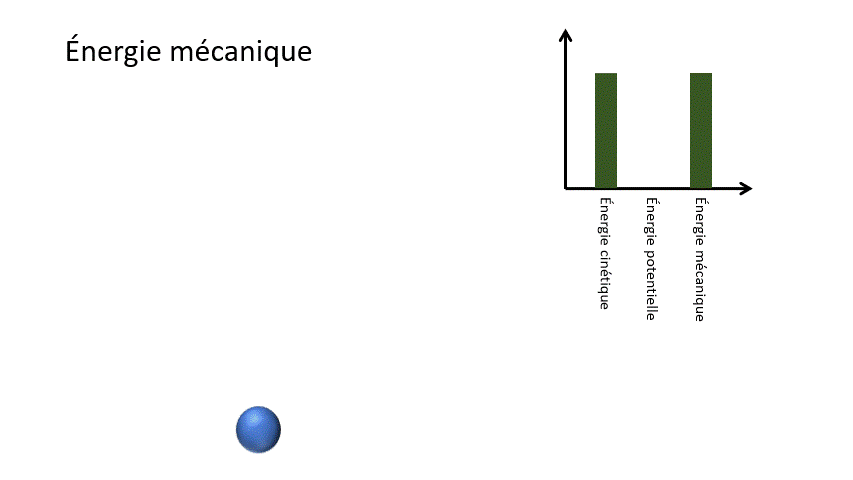
Description

Formule

Em = Ek + Ep

Em : Énergie mécanique (J)
Ek : Énergie cinétique (J)
Ep : Énergie potentielle (J)

2.2 Exemples

Exemple 1

Un homme tient une boîte du haut de la fenêtre de son appartement situé au 5ième étage. La boîte en question pèse 15 kg et la hauteur de la fenêtre est à environ 30 mètres du sol. S'il laisse tomber la boîte, quelle sera l'énergie cinétique de la boite à 10 m du sol ?

m = 15 kg
g = 9,8N/kg
h1 = 30 m 
h2 = 10 m
Ek1 = 0J
Ek2 = ?
1. Calcul de l'énergie potentielle à 30 m
Ep1 = mgh1

Ep1 = 15 kg x 9,8 N/kg x 30 m = 4 410 J

2. Calcul de l'énergie potentielle à 10 m
Ep2 = mgh2

Ep2 = 15 kg x 9,8 N/kg x 10 m = 1470 J

3. Calcul de l'énergie cinétique à 10 m
Comme il y a conservation de l'énergie, on peut dire que :
Em1 = Em2
Ek1 + Ep1 = Ek2 + Ep2
0 J + 4 410 J = Ek2 + 1470 J
Ek2 = 4 410 J - 1 470 J = 2 940 J

Exemple 2
Quelle sera la vitesse de la boîte lorsqu'elle atteindra le sol ?

m = 15 kg
g = 9,8N/kg
h1 = 30 m
Ep2 = 0J
Ek1 = 0J
v2 = ?

1. Calcul de l'énergie cinétique au sol
Comme il y a conservation de l'énergie, on peut dire que :
Em1 = Em2
Ek1 + Ep1 = Ek2 + Ep2
0 J + 4 410 J = Ek2 + 0 J
Ek2 = 4 410 J

2. Calcul de la vitesse
Ek2 = ½ mv2²
4 410 J = ½ x 15 kg x v2²
392 = v22
v2 = \(\huge{  \sqrt[]{392} m/s }\)
v = 19,8 m/s

Les utilisateurs invités n’ont pas la permission d’interagir avec des questions intégrées.

Les utilisateurs invités n’ont pas la permission d’interagir avec des questions intégrées.

Clique sur le bouton ci-dessous afin de poursuivre au chapitre suivant.

Continuer   

4. Lien entre travail et énergie

Pour finir, concentrons-nous sur ce qui permet au pendule de commencer son mouvement. Pour faire monter le pendule à sa hauteur maximale, on doit appliquer une force et effectuer un travail (W). L'énergie consommée par notre main pour faire monter le pendule, notre travail, fourni au pendule une énergie potentielle. Lorsqu'on lâche le pendule, cette énergie potentielle se transforme en énergie cinétique. 

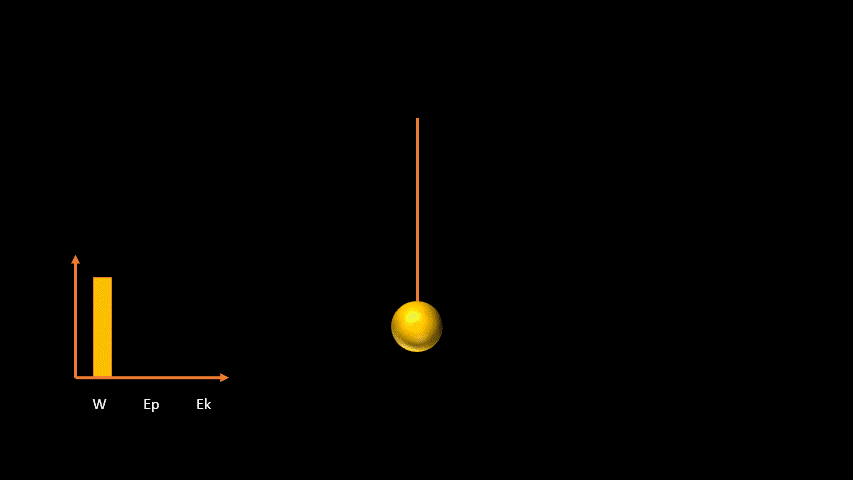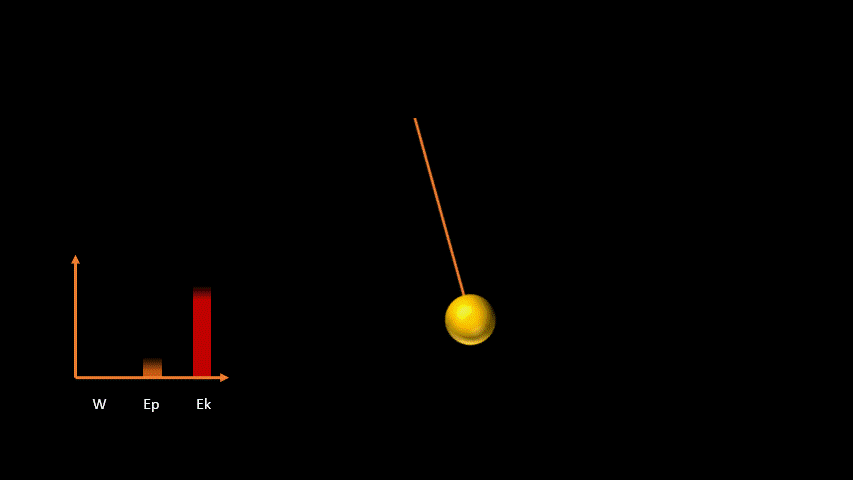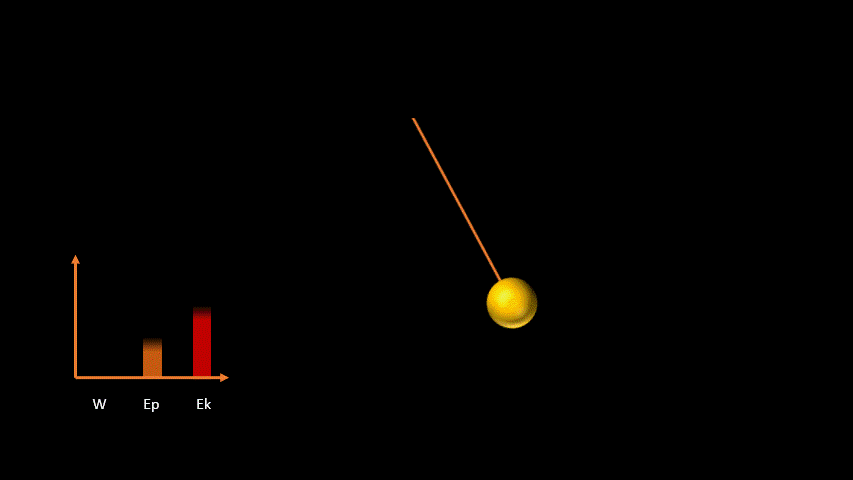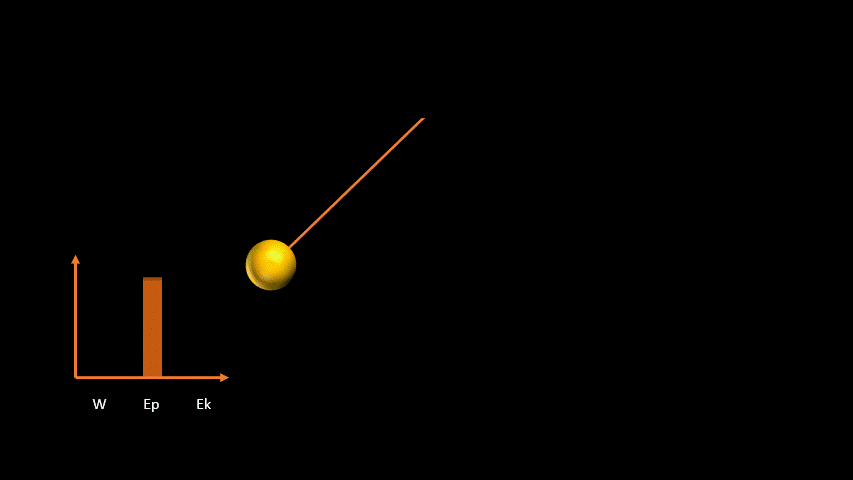
Description


 Comme le travail effectué a été transformée en énergie potentielle (au a augmenté la hauteur de la bille du pendule), on peut dire que :

W = ΔEp

Au plus bas de sa course, le pendule a une grande vitesse, mais sa hauteur est minimale. L'énergie potentielle s'est donc transformée en énergie cinétique. Le principe vu précédemment s’applique donc aussi  pour l’énergie cinétique :

W = ΔEp = ΔEk

On peut donc conclure que tout travail effectué sur un objet sera transformé en énergie.

Formule

W = ΔE

W : Travail (J)
ΔE : Variation d'énergie (J)
Les utilisateurs invités n’ont pas la permission d’interagir avec des questions intégrées.

Les utilisateurs invités n’ont pas la permission d’interagir avec des questions intégrées.


Clique sur le bouton ci-dessous afin de poursuivre au chapitre suivant.

Continuer   

5. Synthèse

Astuce!

Tu veux réussir mieux ! Prends le temps de consigner dans le cahier de note l'ensemble de tes apprentissages. Tu auras ainsi un cahier non seulement ordonné, mais aussi imprimable. De plus, le fait de résumer, d'expliquer, de synthétiser la matière te permet de mieux l'assimiler. Ton temps d'étude en sera sans aucun doute réduit!

Important : Lorsque tu prends des notes dans ton cahier, tu dois toujours cliquer sur "enregistrer" pour les conserver. Une fois tes notes compilées, n'oublie pas de cocher la boite à côté de cette ressource afin d'avoir accès au test de validation de la station.

Voici ce que je retiens de la station 6 : 

Voir mes notes