M6S5_RE (STE)
| Site: | Moodle CSSRDN |
| Cours: | Science 4e secondaire (ST / STE) - 2023-2024 - Douance |
| Livre: | M6S5_RE (STE) |
| Imprimé par: | Visiteur anonyme |
| Date: | jeudi 17 juillet 2025, 02:55 |
Description
Tu dois parcourir l'ensemble des chapitres de ce cahier de ressources pour bien te préparer au test de validation de cette station.
1. Notion de force
Dans cette section, nous prendrons le temps de comprendre ce qu'est une force et quel sera l'impact de l'application d'une force sur un corps.
FORCE
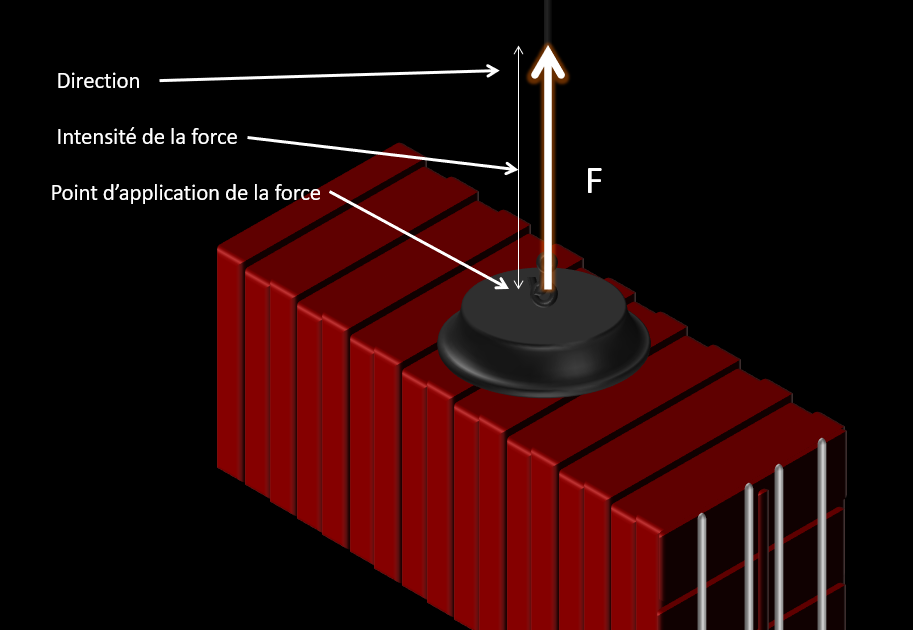
On définit la force comme une action capable de créer ou modifier le mouvement d’un objet. L’unité de mesure de la force est le Newton (N).
Elle est définie par une valeur et une direction. Ainsi, on parle d'une force de 3N vers le bas ou de 5N vers l'est.
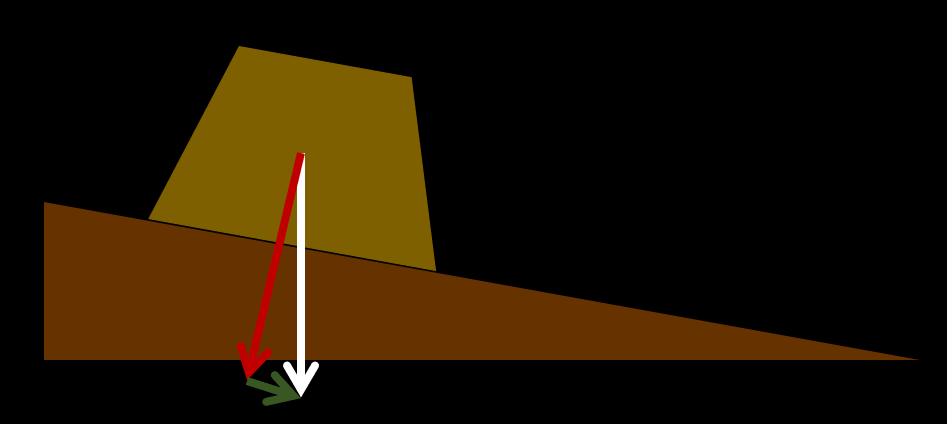
On peut aussi décomposer une force. Par exemple, si on place un bloc sur un plan incliné, on distingue la composante du poids qui est perpendiculaire au plan (celle qui tente d'écraser le plan) et celle qui est parallèle au poids (celle qui tente de faire descendre le bloc le long du plan incliné). Ces deux composantes étant perpendiculaires, on peut utiliser la trigonométrie pour calculer la grandeur de chacune d'entre elles.
Si ces notions de mathématiques sont un peu lointaines, vous pouvez vous rafraîchir la mémoire en consultant la section Coup de pouce en maths.
1.1. La force gravitationnelle
1.1.1 Définition de la force gravitationnelle (Fg)
Formule
Fg = m • g
Fg : Force gravitationnelle (poids) (N)
m : Masse (kg)
g : Accélération gravitationnelle (9,8 N/kg)
On nomme également cette force, le poids. Notre poids est donc la force avec laquelle la Terre nous attire vers elle. Sur une autre planète, notre poids serait donc différent, mais pas notre masse, car celle-ci représente la quantité de matière qui compose un corps. Cette valeur ne varie pas. On dit que la masse est universelle donc la même partout dans l’univers.
1.1.2 Exemples de calcul
Exemple 1
Une boule de bowling qui possède une masse de 3 kg tombe en chute libre. Quelle est la force gravitationnelle qui l’attire vers la Terre?
m = 3kg
g = 9,8 N/kg
Fg = ? N
Fg = m • g
Fg = 3 kg x 9,8 N/kg
Exemple 2
Quel serait le poids de la boule sur Mars (g = 3,73 N/kg) ou sur Jupiter (g = 25,87 N/kg)
Fg = m • g
Fg = 3 kg x 3,73 N/kg
Fg = 11,19 N
Fg = m • g
Fg = 3 kg x 25,87 N/kg
Clique sur le bouton ci-dessous afin de poursuivre à la section suivante.
Continuer1.2. La force normale
1.2.1 La force normale (Fn)
La force normale représente la force de réaction (principe d’action-réaction) d’une surface empêchant un objet de s’enfoncer dans cette surface.
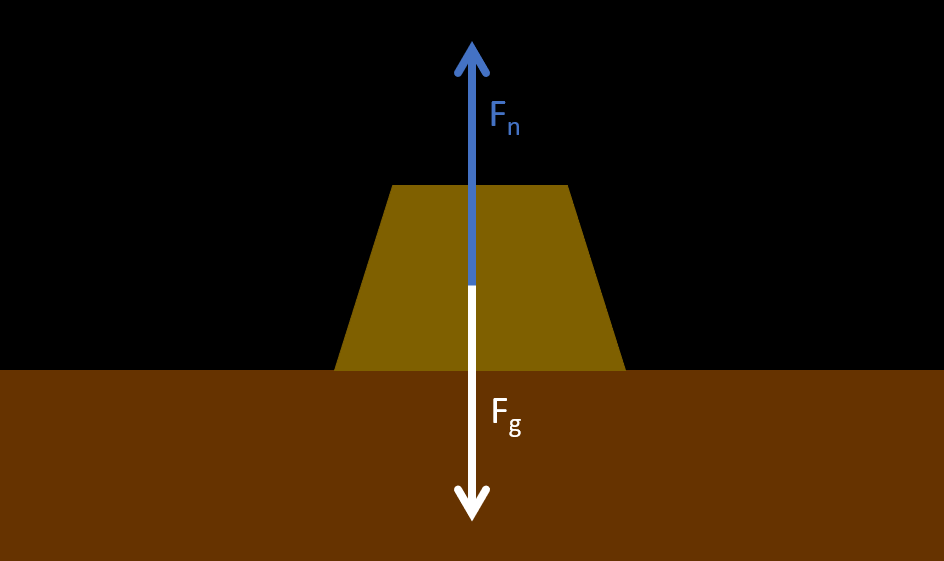
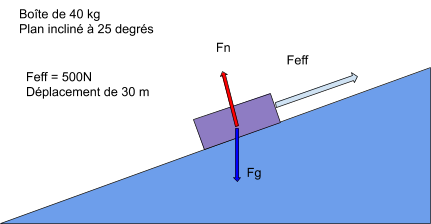
Lorsque la surface est inclinée, la force normale n'est pas égale à la force gravitationnelle, mais plutôt à l'une des composantes (x ou y) de la force gravitationnelle. Dans le cas ci-dessous, la force normale (Fn) va être égale à la composante y (Fgy) de la force gravitationnelle (Fg).
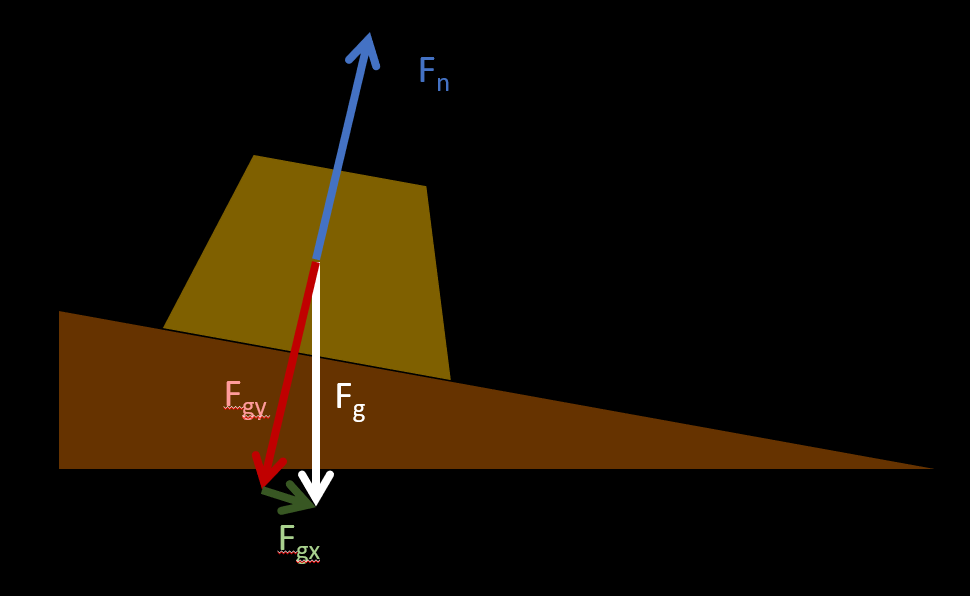
Pour nous l'avons vu dans la section 1, les forces peuvent être décomposées en utilisant la trigonométrie. C'est d'ailleurs pourquoi nous utilisons la fonction cosinus, voir ici ou bien découvre par toi-même avec cette animation.
Pour utiliser l'application, change l'inclinaison du plan avec le curseur « angle ».
Tu peux utiliser l'application suivante pour t'aider à visualiser ce qu'on te demande. Pour utiliser l'application, tu peux changer l'inclinaison du plan ou la masse de l'objet avec le curseur.
1.2.2 Exemple
m = 66 kg
θ = 30°
Fg = ? N
Fn = ? N
Fn = m g cos θ
Fn = 66 kg x 9,8 N/kg x cos 30°
Clique sur le bouton ci-dessous afin de poursuivre à la section suivante.
Continuer1.3. La force de frottement
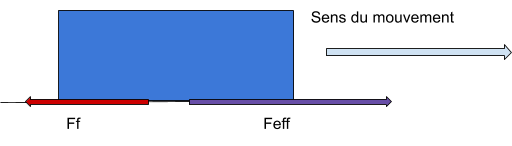
Clique sur le bouton ci-dessous afin de poursuivre à la section suivante.
Continuer
1.4. La force résultante et force équilibrante
1.4.1 La force résultante
Comme on l'a vu, plusieurs forces différentes peuvent s'appliquer simultanément sur un même objet. Ainsi, trois forces s'appliquent sur un objet posé sur un plan incliné, soient la force gravitationnelle (poids de l'objet), la force normale (perpendiculaire au plan) et la force de friction. Dans les exemple que nous avons vu jusqu'à maintenant, le bloc est en équilibre, c'est-à-dire qu'il ne bouge pas. C'est donc dire que les forces appliquées sur l'objet s'annulent ou, si vous préférez, que la somme des forces est nulle. La force résultant (FR) est donc la somme de toutes les forces appliquées. Elle est nulle si l'objet est immobile ou s'il se déplace à vitesse constante sans changer de trajectoire (tourner).
Qu'arriverait-il si la force de frottement entre le bloc et le plan était insuffisante pour garder le bloc en équilibre ? Le bloc glisserait et accélèrerait alors vers le bas du plan incliné et la force résultante ne serait plus égale à zéro. Cette accélération (ou cette décélération) est le signe d'une force résultante non-nulle.
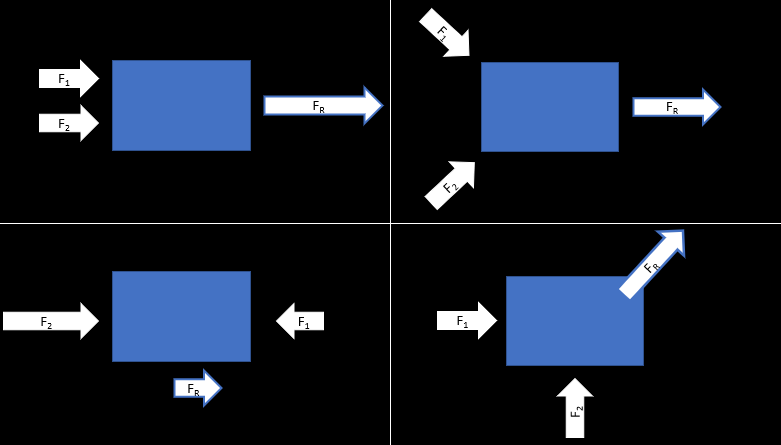
1.4.2 La force équilibrante
Clique sur le bouton ci-dessous afin de poursuivre à la section suivante.
Continuer1.5. La force efficace
1.5.1 La force efficace
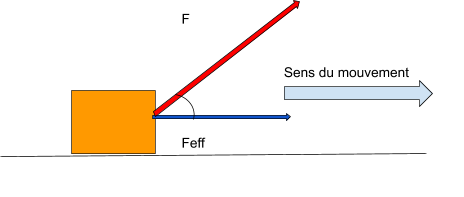
La force efficace est la composante parallèle au mouvement de l’objet. C’est elle qui est responsable du déplacement.
On la calcule par trigonométrie.
Prenons l'exemple d'une locomotive qui accélère en sortant de la gare. Plusieurs forces s'exercent sur lui (force gravitationnelle, force normale, force de frottement, force du moteur), mais globalement, certaines de ses forces s'annulent (la force gravitationnelle et la force normale par exemple), ce qui fait que la force résultante est parallèle au mouvement vers l'avant du train. C'est cette force qu'on appelle la force efficace. La locomotive tire ses wagons et la force qu'elle applique est parallèle au mouvement des wagons. Or, si elle tire une luge (très mauvaise idée), seule la composante qui est parallèle au mouvement sera considérée comme une force efficace.
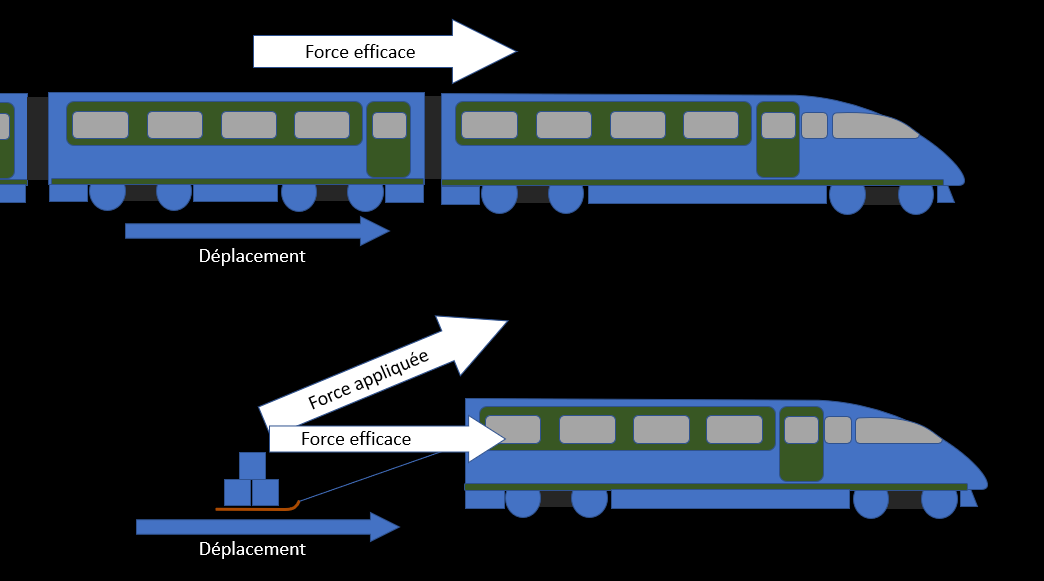
Formule
Feff = F x cos θ
1.5.2 Exemples
Exemple 1
Feff = F x cos 30°
Feff = 50 N x cos 30°
Exemple 2
Feff = 22 N
F = 32 N
θ = ?
Feff = F x cos θ
22 N = 32 N x cos θ
1.5.3 Simulateurs
Tu peux tester l’effet des différentes forces grâce à cette autre animation.
Exercice:
Sur le schéma ci-dessous, place les forces suivantes:- Force gravitationnelle (Fg)
- Force normale (Fn)
- Force de frottement (Ff)
- Force efficace (Feff)
Reproduit ce schéma dans ton cahier de notes et place les flèches qui représentent les forces selon le code de couleur fourni.
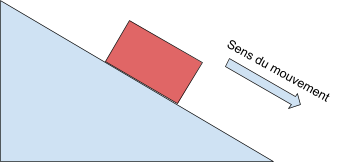
Réponse attendue :
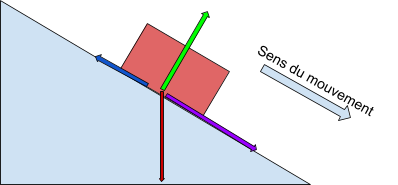
Voici un simulateur qui te permet de jouer avec les différentes forces pour en voir les effets. Notes tes observations dans ton cahier pour référence future.
Clique sur le bouton ci-dessous afin de poursuivre au chapitre suivant.
Continuer2. Travail
2.1 Définition
Le travail se définit comme étant un transfert d’énergie, tout comme la chaleur, mais ici l’effet sera le déplacement d’un objet sur lequel on a exercé assez de force pour le faire bouger dans un sens.
Il y a deux conditions pour que ce transfert d’énergie se produise :
- Une force doit être appliquée sur l’objet et au moins une des composantes de cette force doit pousser dans le sens du mouvement.
- L’objet qui reçoit cette énergie doit être déplacé.
La formule pour calculer le travail est la suivante :
Formule
W = F Δx
2.2 Exemples
Exemple 1
On fait bouger un colis, sur une surface plane, jusqu’à qu’il soit à 7 m de sa position d’origine. La force nécessaire pour y arriver est de 58 N. Quel travail a-t-on effectué si on néglige la force de frottement?
W = F Δx
Il est important de noter que dans cet exemple la force et le déplacement sont parallèles. Si les deux ne sont pas parallèles, il faut trouver la composante de la force qui va dans la même direction que le mouvement tout comme c’est le cas avec le calcul de la force efficace.
Exemple 2
Refais ce schéma dans ton cahier avec dessins de toutes les forces en jeu. (On considère qu’il n’y a pas de frottement). Calcule ensuite la force gravitationnelle, la force normale et le travail nécessaire pour faire avancer la boîte de 30 m. Prends bien soin de noter toutes tes démarches.
Fg = 40 kg x 9,8 N/kg
Fn = Fg x cos θ
Fn = 355 N
W = Feff Δx
Exemple 3
Notre bonhomme tire sur la corde du traîneau avec un angle de 35° et une force de 50 N. Quel sera le travail effectué par celui-ci sur une distance de 2 km? (On considère qu’il n’y a pas de frottement). N’oublie pas que la force efficace est toujours parallèle au mouvement.
Feff = F x cos θ
Fn = 41 N
W = Feff Δx
Clique sur le bouton ci-dessous afin de poursuivre au chapitre suivant.
Continuer3. Synthèse
Astuce!
Tu veux réussir mieux ! Prends le temps de consigner dans le cahier de note l'ensemble de tes apprentissages. Tu auras ainsi un cahier non seulement ordonné, mais aussi imprimable. De plus, le fait de résumer, d'expliquer, de synthétiser la matière te permet de mieux l'assimiler. Ton temps d'étude en sera sans aucun doute réduit!
Important : Lorsque tu prends des notes dans ton cahier, tu dois toujours cliquer sur "enregistrer" pour les conserver. Une fois tes notes compilées, n'oublie pas de cocher la boite à côté de cette ressource afin d'avoir accès au test de validation de la station.