M6S4_RE (STE)
| Site: | Moodle CSSRDN |
| Cours: | Science 4e secondaire (ST / STE) - 2023-2024 - Douance |
| Livre: | M6S4_RE (STE) |
| Imprimé par: | Visiteur anonyme |
| Date: | vendredi 16 janvier 2026, 19:59 |
Description
Tu dois parcourir l'ensemble des chapitres de ce cahier de ressources pour bien te préparer au test de validation de cette station.
1. Le calorimètre
Il existe un appareil conçu spécifiquement pour trouver la quantité d’énergie thermique transférée d’une substance à une autre. Il s’agit d’un calorimètre.
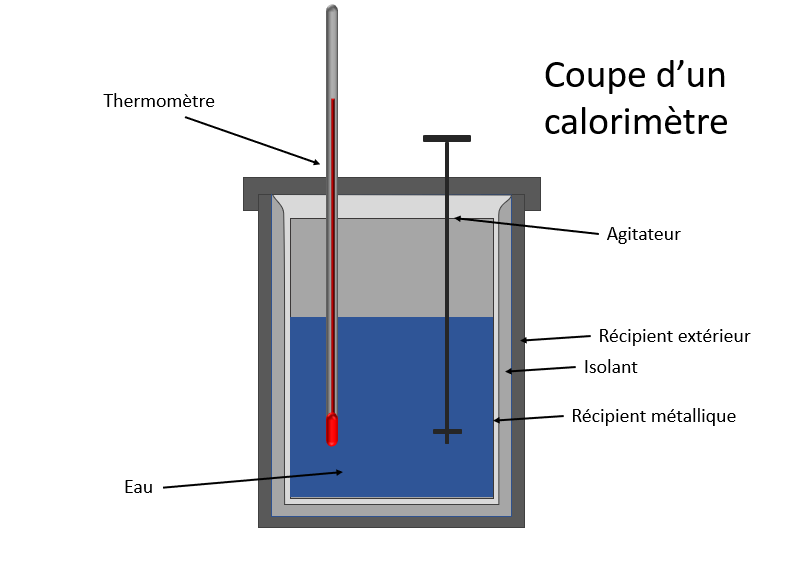
Il en existe des différents, mais celui qui nous aidera est un modèle comme illustré dans le schéma ci-dessus. Son principe de fonctionnement est assez simple.
On a un premier contenant (le récipient extérieur) qui en contient un plus petit (le récipient métallique). Généralement ils sont faits d’aluminium. Les deux sont séparés par un isolant (en mousse ou autre). Le couvercle a deux petits trous, un pour le thermomètre et un autre pour l’agitateur qui servira à bien répartir la chaleur dans le liquide.
On mesure soigneusement la quantité du liquide ainsi que sa température initiale, ensuite on plonge un bloc de la substance inconnue qu’on sera préalablement chauffée. On ferme hermétiquement le tout et on laisse la température monter tout en agitant doucement le liquide. Lorsque que la température sera stabilisée jusqu’à un maximum, on prend en note celle-ci. Comme il s’agit d’un système isolé, presque toute l’énergie transférée passera du bloc au liquide jusqu'à ce que la température soit uniforme dans tout le calorimètre.
2. Calcul de l'énergie thermique absorbée par une substance
2.1 Formule à utiliser pour calculer l'énergie thermique
L’énergie thermique est l'énergie liée au déplacement et à l'agitation des particules qui composent la matière. Elle est proportionnelle à la masse de la substance, à la nature de celle-ci et à l’écart de température observée. Pour calculer l’énergie absorbée ou dégagée par la substance, on utilise la formule suivante :
Formule
Q = m c ΔT
2.2 Exemple
On fait chauffer 750 g d’eau à 10℃ jusqu’au point d’ébullition (100℃). Quelle quantité d’énergie thermique l’eau a-t-elle absorbée ?
Q = mc ΔT
Q = 750g x 4,19 J/g℃ x (100℃ - 10℃)
Q = 282 825 J
Clique sur le bouton ci-dessous afin de poursuivre au chapitre suivant.
Continuer3. Transfert d'énergie d'une substance à une autre
3.1 Les transferts d'énergie et les conventions
Comme nous l’avons vu dans la section sur la conservation de l’énergie, il n’y a pas de perte, ni de création d’énergie. Ainsi, si un corps refroidit, c'est qu'il a transféré son énergie à son environnement. Dans un calorimètre, cet environnement est de l'eau. Ainsi, on a un milieu contrôlé complètement isolé qui permet de mesurer précisément la quantité d'énergie qui a été transférée en mesurant la variation de température de l'eau. Comme on connait la capacité thermique massique et la masse de l'eau qu'on a versé dans le calorimètre, le calcul devient similaire à celui que nous avons fait à la page précédente.
Par convention, nous avons une valeur positive de l'énergie (Q) quand il s’agit d’une absorption de chaleur et une valeur négative de l'énergie (Q) quand c’est un dégagement de chaleur. Si le bloc de nature inconnue est plus chaud que l'eau contenue dans le calorimètre, le flux de chaleur passera du bloc à l'eau et celle-ci verra sa température augmenter. Inversement, si le bloc de nature inconnue est plus froid que l'eau contenue dans le calorimètre, le flux de chaleur passera de l'eau au bloc. La température de l'eau diminuera.

Formule
Qabsorbée = -Qdégagée
Comment sera-t-il possible de trouver une substance inconnue à partir d’ici ? Encore une fois, tu trouveras ici la liste des capacités thermiques massiques de différentes substances.
3.2 Exemples
Exemple 1
On plonge une bague d'or dans 10 g d'eau. La température de l'eau augmente de 2 ℃, puis se stabilise. Quelle est la masse de la bague? On estime que la température de la bague a diminuée de 43,3℃.
meau = 10g
ceau = 4,19 J/g℃
ΔTeau = 2 ℃
ΔTor = - 43,3℃
cor = 0,129 J/g℃
mor = ? g
\( \Large{Q_{absorbée} = - Q_{dégagée}} \)
\( \Large{m_{eau} \times c_{eau} \times ΔT_{eau} = - m_{or} \times c_{or} \times ΔT_{or} } \)
\( \Large{ 10 g \times 4,19 J/g℃ \times 2 ℃ = - m_{or} \times 0,129 J/g℃ \times (- 43,3℃)} \)
\( \Large{ m_{or} = \frac{10 g \times 4,19 J/g℃ \times 2 ℃}{0,129 J/g℃ \times 43,3℃} } \)
\( \Large{ m_{or} = 15g } \)
Exemple 2
On plonge un cube de 15 g de cuivre (0,385 J/g℃) dans 200 g d'eau . Si l'eau est initialement à 25℃ et le cube, à 125℃, quelle sera la température finale du mélange ?
meau = 200 g
ceau = 4,19 J/g℃
Tieau = 25 ℃
Ticuivre = 125℃
ccuivre = 0,385 J/g℃
mcuivre = 15 g
Tf = ? ℃
\( \Large{Q_{absorbée} = - Q_{dégagée}} \)
\( \Large{m_{eau} \times c_{eau} \times ΔT_{eau} = - m_{Cu} \times c_{Cu} \times ΔT_{Cu} } \)
\( \Large{10 g \times 4,19 J/g℃ \times (T_f - 25℃) = - 15 g \times 0,285 J/g℃ \times (T_f - 125℃)} \)
\( \Large{41,9 T_f - 1047,5 = - 4,275 T_f + 534,4} \)
\( \Large{46,175 T_f = 1581,9} \)
\( \Large{ T_f = 34,26 ℃} \)
Clique sur le bouton ci-dessous afin de poursuivre au chapitre suivant.
Continuer4. Synthèse
Astuce!
Tu veux réussir mieux ! Prends le temps de consigner dans le cahier de notes l'ensemble de tes apprentissages. Tu auras ainsi un cahier non seulement ordonné, mais aussi imprimable. De plus, le fait de résumer, d'expliquer, de synthétiser la matière te permet de mieux l'assimiler. Ton temps d'étude en sera sans aucun doute réduit!
Important : Lorsque tu prends des notes dans ton cahier, tu dois toujours cliquer sur "enregistrer" pour les conserver. Une fois tes notes compilées, n'oublie pas de cocher la boite à côté de cette ressource afin d'avoir accès au test de validation de la station.