M6S6_RE (STE)
3. L'énergie mécanique
3.1 Définition de l'énergie mécanique
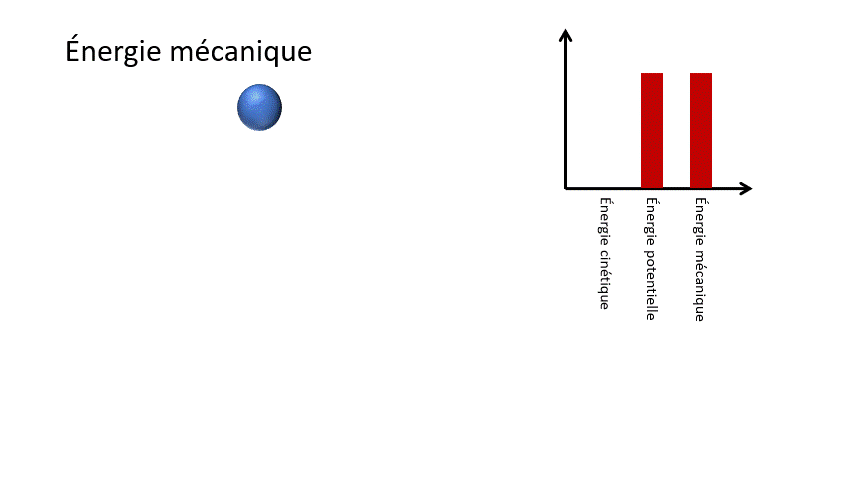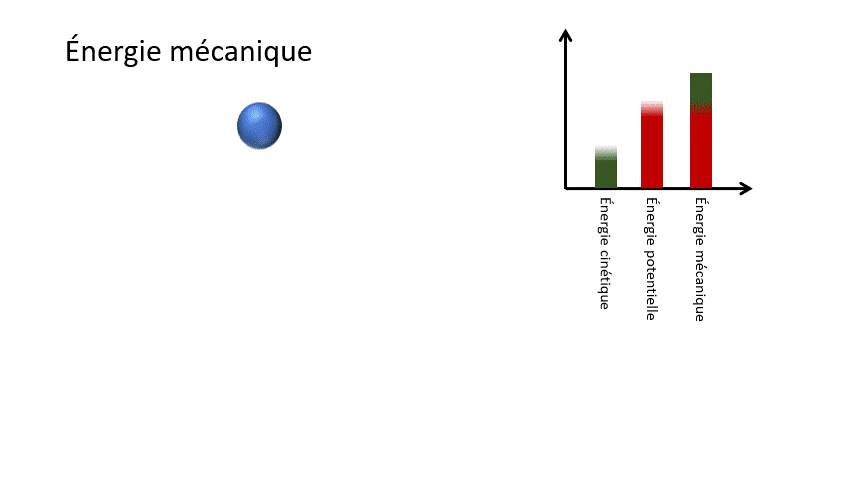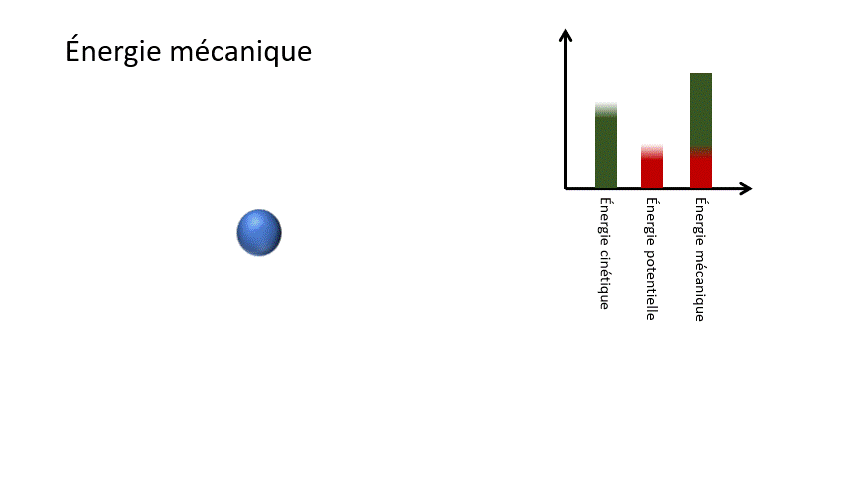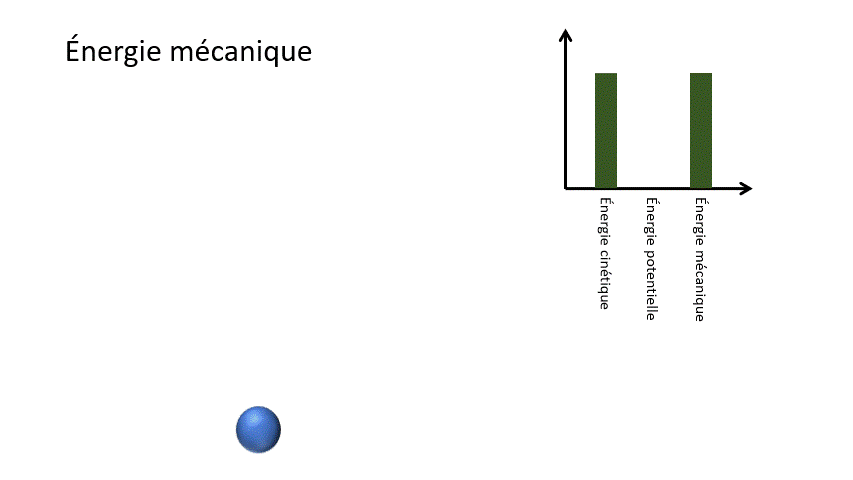
Pour un corps en chute libre, l'énergie potentielle gravitationnelle liée à la hauteur de l'objet est transformée en énergie cinétique liée à la vitesse de celui-ci. Ainsi, l'objet accélère dans sa chute.
Formule
Em = Ek + Ep
Em : Énergie mécanique (J)
Ek : Énergie cinétique (J)
Ep : Énergie potentielle (J)
2.2 Exemples
Exemple 1
Un homme tient une boîte du haut de la fenêtre de son appartement situé au 5ième étage. La boîte en question pèse 15 kg et la hauteur de la fenêtre est à environ 30 mètres du sol. S'il laisse tomber la boîte, quelle sera l'énergie cinétique de la boite à 10 m du sol ?
m = 15 kg
g = 9,8N/kg
h1 = 30 m
h2 = 10 m
Ek1 = 0J
Ek2 = ?
1. Calcul de l'énergie potentielle à 30 m
Ep1 = mgh1
Ep1 = 15 kg x 9,8 N/kg x 30 m = 4 410 J
2. Calcul de l'énergie potentielle à 10 m
Ep2 = mgh2
Ep2 = 15 kg x 9,8 N/kg x 10 m = 1470 J
3. Calcul de l'énergie cinétique à 10 m
Comme il y a conservation de l'énergie, on peut dire que :
Em1 = Em2
Ek1 + Ep1 = Ek2 + Ep2
0 J + 4 410 J = Ek2 + 1470 J
Ek2 = 4 410 J - 1 470 J = 2 940 J
Exemple 2
Quelle sera la vitesse de la boîte lorsqu'elle atteindra le sol ?
m = 15 kg
g = 9,8N/kg
h1 = 30 m
Ep2 = 0J
Ek1 = 0J
v2 = ?
1. Calcul de l'énergie cinétique au sol
Comme il y a conservation de l'énergie, on peut dire que :
Em1 = Em2
Ek1 + Ep1 = Ek2 + Ep2
0 J + 4 410 J = Ek2 + 0 J
Ek2 = 4 410 J
2. Calcul de la vitesse
Ek2 = ½ mv2²
4 410 J = ½ x 15 kg x v2²
392 = v22
v2 = \(\huge{ \sqrt[]{392} m/s }\)
v = 19,8 m/s